Torque is the rotational equivalent of linear force
Torque Density is a performance measure of a components torque force against its mechanical parameters.
Within context of robotic manipulators, torque density refers to the capability of an actuator to lift a specified amount at a given extension compared with its size and weight. It is accepted that a large, heavy manipulator can lift more than a smaller, lighter one. In the area of field robotics lifting more with a smaller system improves capability and portability, extending the overall usefulness of the system. Tasks such as rotating valves, station keeping the vehicle in current and recovering heavy objects from the seabed all benefit from a manipulator with more torque but compact enough to not significantly impact the performance of the vehicle.
Torque Load & Lift Capacity of a Manipulator
A key specification of a robotic manipulator is lifting capacity. This is often specified at some distance from the base such as at full reach or a fraction thereof. The more a manipulator can lift the more work it is able to do and the more robust it will be when subjected to external loads.
Each joint on the manipulator experiences a different torque load depending how close to the end effector it is positioned. Ones at the base require the highest torque, whereas the wrist joints near the gripper require the least. Joints at the base do not only need to lift the specified weight but they also need to lift the weight of the manipulator. It is therefore important that the actuators closer to the end are as light as possible while still being able to provide the required torque. If they are not their weight will limit the practical reach of the manipulator. In most applications it is desirable to have the manipulator be as light as possible while being able to lift a significant weight at the desired reach. In the example below J1 torque requirement is made up of the load mass (M1) plus the mass of the second actuators (J2) multiplied by their respective distances. J2 also has torque requirement which is dictated by the load mass (M1) multiplied by distance (D2). It is evident from this example that joint J2 needs to achieve its torque specification without becoming too heavy. As its weight is increased the remaining torque to lift the payload is decreased. This problem is exasperated when considering the more realistic situation of multiple joints, up to 7 in the case of Reach X.

Torque required for J2 = M1 x D2 = 14.7Nm; Torque required for J1 = M1 x (D1+D2) + M2 x (D1) = 32.3Nm

How is it defined?
Comparing the torque of an actuator to its size and weight (Nm/g or Nm/mm^3) provides a good indication of performance. In some applications it is relevant to include velocity such as when a particular load is required to be moved at speed. When including this term, we get the power per weight and size of the actuator (W/g or W/mm^3) which is a more comprehensive indication of performance, rarely provided on datasheets. A higher value means the manipulator will be able to lift more or move faster while weighing less or occupying less space. Torque and velocity have an inverse relationship dictated by the motor parameters and the damping factors within the gearbox. This can be as seen on the graph below highlighting the importance of the power density calculation as specifying a torque may indicate that it is achievable but only at a very low velocity which is of limited use.
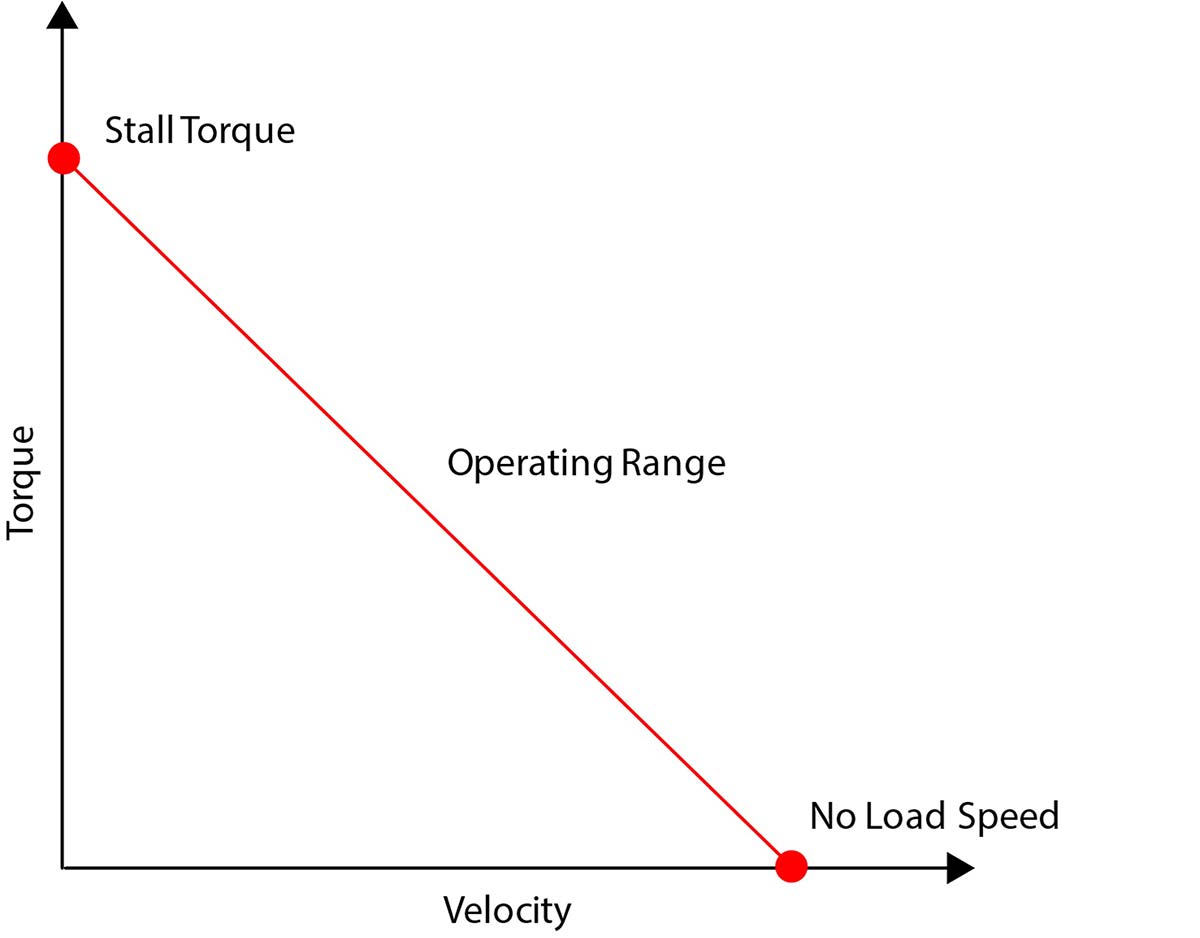
For an example the Reach X F Joint, which has the highest torque requirement, has a max torque of 36Nm at 40 degrees per second (0.7rad/s), a volume of 2750mm3 and a mass of 330g. This gives it a torque density of 0.0131Nm/mm3 or 0.11Nm/g. The power density is 0.0091W/mm3 or 0.076W/g noting that this is mechanical power, a more relevant term than electrical power.
Factors in increasing Power Density
As apparent from the units increasing the power density of an actuator can be achieved by either increasing the output torque or velocity or by decreasing the volume or mass. When designing high performance actuators some of these terms are set according to external factors such as the maximum payload of the host vehicle or the required torque for rotating a valve. Once one is set the challenge is to optimise the other as far as possible to achieve maximum performance.
Torque is most often limited by the gearbox which in turn is dictated by the size and type of gears selected such as strain wave gearing, cycloidal or planetary. The motor makes up a sizeable portion of the volume and mass and therefor selecting one that can saturate the gearbox but remains compact is a critical part of the design process. Once motor and gearbox have been paired other factors such electronics, sliprings and heat dissipation all need to be considered to ensure the required output power can be obtained and the footprint and weight budget is adhered to.







